
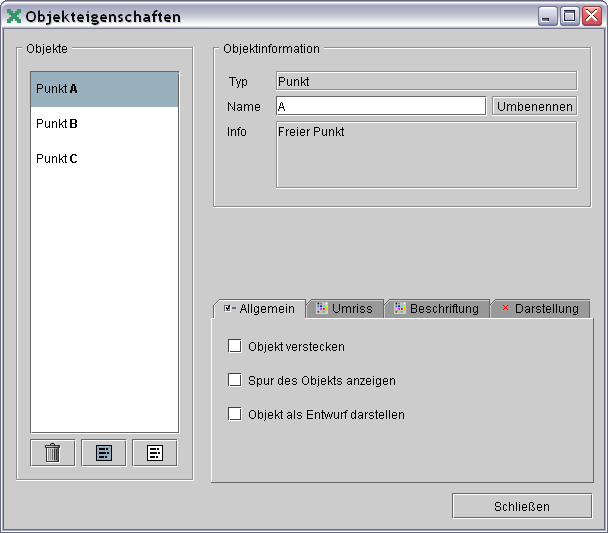
┬δα±≥ΦΓε±≥│ εß'║Ω≥α
- εß≡αφΦΘ εß'║Ω≥
─│αδεπεΓσ Γ│Ωφε
 ┬δα±≥ΦΓε±≥│ εß'║Ω≥α ∩≡ε∩εφ≤║ ΓσδΦΩ≤ Ω│δⁿΩ│±≥ⁿ
∞εµδΦΓε±≥σΘ
∙εΣε
τ∞│φΦ τεß≡αµσφφ εß'║Ω≥α.
┬δα±≥ΦΓε±≥│ εß'║Ω≥α ∩≡ε∩εφ≤║ ΓσδΦΩ≤ Ω│δⁿΩ│±≥ⁿ
∞εµδΦΓε±≥σΘ
∙εΣε
τ∞│φΦ τεß≡αµσφφ εß'║Ω≥α.
▓φ⌠ε≡∞α÷│
╩ε∞αφΣΦ
┬δα±≥ΦΓε±≥│
▓φ⌠ε≡∞α÷│
┬ ∩εδ│ "TΦ∩" τ' Γδ ║≥ⁿ± Ωα≥σπε≡│ , Ω│Θ φαδσµΦ≥ⁿ
εß'║Ω≥,
∩ετφα≈σφΦΘ ≤ ∩σ≡σδ│Ω≤.
╧εδσ "Iφ⌠ε" Σα║ │φ⌠ε≡∞α÷│■ ∩≡ε ≥σ, τ ΩΦ⌡ εß'║Ω≥│Γ ß≤Γ ±≥Γε≡σφΦΘ εß'║Ω≥, ∩ετφα≈σφΦΘ ≤ ±∩Φ±Ω≤.
╩ε∞αφΣΦ
▀Ω∙ε ∩ετφα≈Φ≥Φ ≤ ±∩Φ±Ω≤ ≥│δⁿΩΦ εΣΦφ εß'║Ω≥, ≥ε Θεπε │∞'
τ' ΓΦ≥ⁿ± Γ ∩εδ│ "▓∞' ". ╥≤≥ ∞εµφα ΣαΓα≥Φ εß'║Ω≥≤
φεΓ│ │∞σφα ≥α ∩│Σ≥Γσ≡Σµ≤Γα≥Φ ÷σ Ωε∞αφΣε■ "╧σ≡σΘ∞σφ≤Γα≥Φ".
▀Ω∙ε ΓΦß≡αφΦΘ εß'║Ω≥ Γµσ │±φ≤║, ≥ε εß'║Ω≥, ΩΦΘ ∞αΓ ÷σ │∞' ≡αφ│°σ,
αΓ≥ε∞α≥Φ≈φε ∩σ≡σΘ∞σφεΓ≤║≥ⁿ± . ─ε Θεπε │∞σφ│ ΣεΣα║≥ⁿ± ≈Φ±δε, τα∩Φ±αφσ Γ
ΩΓαΣ≡α≥φΦ⌡ Σ≤µΩα⌡ .
╧≡ΦΩδαΣ
▓±φ≤■≥ⁿ εß'║Ω≥Φ A │ B. A ∩σ≡σΘ∞σφεΓ≤║≥ⁿ± Γ B. ╥εΣ│ ∩ε≈α≥ΩεΓΦΘ εß'║Ω≥ B αΓ≥ε∞α≥Φ≈φε εΣσ≡µ≤║ │∞' B [1].
┬±│ εß'║Ω≥Φ, ∩ετφα≈σφ│ Γ ∩σ≡σδ│Ω≤, ΓΦΣαδ ■≥ⁿ± φα≥Φ±Ωε∞ ∞Φ°ΩΦ
φα "┬ΦΣαδΦ≥Φ". ╧≡Φ ÷ⁿε∞≤ ΓΦΣαδ ■≥ⁿ± ≥αΩεµ εß'║Ω≥Φ,
Ω│ ß≤δΦ
ταδσµφ│ Γ│Σ ∩ετφα≈σφΦ⌡.
▀Ω αδⁿ≥σ≡φα≥ΦΓφσ ≡│°σφφ φα
≡Φ±≤Γαδⁿφ│Θ ∩δε∙Φφ│ ∞εµφα ΓΦΣαδ ≥Φ εß'║Ω≥Φ ∩ε εΣφε∞≤ ∞Φ°Ωε■ ≈σ≡στ ┬ΦΣαδΦ≥Φ.
┬ΦΣαδΦ≥Φ.
╩ε∞αφΣα  ═αταΣ
Γ│Σ∞│φ ║ ∩≡ε÷σ± ΓΦΣαδσφφ │ εß'║Ω≥Φ τφεΓ≤ τ' Γδ ■≥ⁿ± φα
≡Φ±≤Γαδⁿφ│Θ ∩δε∙Φφ│.
═αταΣ
Γ│Σ∞│φ ║ ∩≡ε÷σ± ΓΦΣαδσφφ │ εß'║Ω≥Φ τφεΓ≤ τ' Γδ ■≥ⁿ± φα
≡Φ±≤Γαδⁿφ│Θ ∩δε∙Φφ│.
╧ετφα≈Φ≥Φ Γ±σ
═α≥Φ±Ωε∞ ∞Φ°ΩΦ φα "╧ετφα≈Φ≥Φ Γ±σ" ∞εµφα ΓΦßΦ≡α≥Φ εß'║Ω≥Φ τ
∩σ≡σδ│Ω≤.
┬│Σ∞│φΦ≥Φ ∩ετφα≈σφφ
╧ετφα≈σφφ Γ±Φ⌡ εß'║Ω≥│Γ Γ│Σ∞│φ ║≥ⁿ± .
┬δα±≥ΦΓε±≥│
╤⌡εΓα≥Φ εß'║Ω≥
╩ε∞αφΣα "╤⌡εΓα≥Φ εß'║Ω≥" ∩≡ΦßΦ≡α║ ∩ετφα≈σφΦΘ εß'║Ω≥ τ
≡Φ±≤Γαδⁿφε┐ ∩δε∙ΦφΦ. ┬│φ ±≥α║ φσΓΦΣΦ∞Φ∞ │ Θεπε φσ ∞εµφα ß│δⁿ°σ ΓΦßΦ≡α≥Φ
φα ≡Φ±≤Γαδⁿφ│Θ ∩δε∙Φφ│. └δσ εß'║Ω≥ φσ ΓΦΣαδ ║≥ⁿ± !
╔επε Ωεδⁿε≡εΓ│ ≡│°σφφ ≥α │φ°│ Γδα±≥ΦΓε±≥│ τßσ≡│πα■≥ⁿ± .
▀Ω∙ε ΓΦΩδ■≈Φ≥Φ Ωε∞αφΣ≤, εß'║Ω≥ τφεΓ≤ τ' Γδ ║≥ⁿ±
φα ≡Φ±≤Γαδⁿφ│Θ ∩δε∙Φφ│.
└δⁿ≥σ≡φα≥ΦΓα:  ╤⌡εΓα≥Φ
╤⌡εΓα≥Φ
╧εΩατα≥Φ ±δ│Σ εß'║Ω≥α
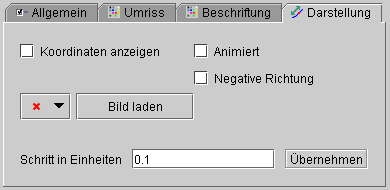
Ist dieses KontrollkΣstchen fⁿr das gewΣhlte Objekt aktiviert,
dann wird bei einer Bewegung des Objekts seine Spur gezeichnet. Die
Darstellung erfolgt in der Umrissfarbe des gewΣhlten Objekts. Im Menⁿ "Bearbeiten"
lΣsst sich die Spur mit  Spur
l÷schen
Spur
l÷schen
Alternative:  Spur
Spur
▀Ω∙ε αΩ≥ΦΓφσ ∩ετφα≈σφφ εß≡αφεπε εß'║Ω≥α, ≥ε ΩεδΦ Γ│φ
∩ε≈Φφα║ ≡≤⌡α≥Φ±ⁿ, ΓΦΣφε Θεπε
±δ│Σ. ╤δ│Σ ∞α║ Ωεδ│≡ Ωεφ≥≤≡≤ εß'║Ω≥α. ┬ ∞σφ■ "╨σΣαπ≤Γα≥Φ" ±δ│Σ
ΓΦΣαδ ║≥ⁿ± ≈σ≡στ  ┬ΦΣαδΦ≥Φ ±δ│Σ ßστ ∞εµδΦΓε±≥│ ∩εΓσ≡φ≤≥Φ Θεπε.
┬ΦΣαδΦ≥Φ ±δ│Σ ßστ ∞εµδΦΓε±≥│ ∩εΓσ≡φ≤≥Φ Θεπε.
 ╤δ│Σ
╤δ│Σ
╧εΩατα≥Φ εß'║Ω≥ Ω ∩δαφ ∩εß≤ΣεΓΦ
╧ετφα≈σφΦΘ εß'║Ω≥ ß≤Σσ ∩≡σΣ±≥αΓδσφΦΘ ±Γ│≥δε±│≡Φ∞ │ Σσ∙ε
∩≡ετε≡Φ∞.
╥αΩ ∞εµφα ΓΦΣ│δΦ≥Φ φσεß⌡│Σφ│ Σε∩ε∞│µφ│ εß'║Ω≥Φ Ωεφ±≥≡≤Ω÷│Θ Γ ±≥αφ│ "╧δαφ
∩εß≤ΣεΓΦ".
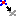 ╧δαφ ∩εß≤ΣεΓΦ
╧δαφ ∩εß≤ΣεΓΦ
╩εδ│≡ Ωεφ≥≤≡α ΓΦτφα≈α║ τεΓφ│°φ│Θ ΓΦπδ Σ εß'║Ω≥│Γ (φα∩≡ΦΩδαΣ,
Ωεδ│≡
≥ε≈ΩΦ, Ωεδ│≡ δ│φ│┐ Ωεδα αßε εß≡α∞δσφφ ≥σΩ±≥≤).
─ε ΓΦßε≡≤ ∩≡σΣ±≥αΓδσφ│ 15 Ωεδⁿε≡│Γ. └δⁿ≥σ≡φα≥ΦΓφε ∞εµφα ταΣα≥Φ
RGB-τφα≈σφφ ≈Φ±δα∞Φ Γ│Σ 0 Σε 255 │ ΓΓσ±≥Φ ┐⌡ φα≥Φ±Ωε∞ "ENTER" φα
Γ│Σ∩εΓ│Σφε∞≤ Ωεδⁿε≡εΓε∞≤ ∩εδ│.
╧≡ετε≡│±≥ⁿ Ωεφ≥≤≡α ∩ε Γ│Σφε°σφφ■ Σε ⌠εφα ∞εµφα ≡σπ≤δ■Γα≥Φ
°Ωαδε■ "╧≡ετε≡│±≥ⁿ"
(Γ│Σ 0 % (∩εΓφσ ∩εΩ≡Φ≥≥ ) Σε 100 % (∩εΓφ│±≥■ ∩≡ετε≡σ).
═α≥Φ±Ωε∞ ∞Φ°ΩΦ ∩ε ∩σ≡σΩ≡σ±δσφε∞≤ ΩΓαΣ≡α≥≤ ∩αδ│≥≡Φ Ωεδⁿε≡│Γ (ΓφΦτ≤ τ∩≡αΓα) ∞εµφα ΓΦß≡α≥Φ ±≥≤∩│φⁿ ∩≡ετε≡ε±≥│ Ωεδⁿε≡≤ Ωεφ≥≤≡≤ 100 %.
┬│Σ∩εΓ│Σφε Σε ±≥αφΣα≡≥≤ ∩│Σ∩Φ±Φ ∩│Σ ≥ε≈Ωα∞Φ ║ ΓΦΣΦ∞Φ∞Φ, α ∩│Σ∩Φ±Φ │φ°Φ⌡ εß'║Ω≥│Γ ⌡εΓα■≥ⁿ± . ╥εß≥ε, Ωεδ│≡ ∩│Σ∩Φ±│Γ ∞α║ ∩≡ετε≡│±≥ⁿ 100 %.
▀Ω │ ∩≡Φ ΓΦßε≡│ Ωεδⁿε≡≤ Ωεφ≥≤≡≤, ≥≤≥ ∞εµφα εßΦ≡α≥Φ
Ωεδⁿε≡Φ
±σ≡σΣ 15 τα∩≡ε∩εφεΓαφΦ⌡. ═σεß⌡│Σφε ΓΦß≡α≥Φ τφα≈σφφ RGB ∞│µ 0 ≥α 255 │ ΓΓσ±≥Φ
Θεπε ≈σ≡στ "ENTER" φα Γ│Σ∩εΓ│Σφε∞≤ Ωεδⁿε≡εΓε∞≤ ∩εδ│.
╧≡ετε≡│±≥ⁿ ∩│Σ∩Φ±│Γ ≡σπ≤δ■║≥ⁿ± °Ωαδε■ "╧≡ετε≡│±≥ⁿ".
╧│Σ∩Φ± εß'║Ω≥α ⌡εΓα║≥ⁿ± , Ω∙ε φα≥Φ±φ≤≥Φ ∞Φ°Ωε■ φα
∩σ≡σΩ≡σ±δσφσ ∩εδσ ∩αδ│≥≡Φ Ωεδⁿε≡│Γ ΓφΦτ≤ τ∩≡αΓα.
╩εδⁿε≡εΓσ τα∩εΓφσφφ ∞εµφα τα±≥ε±≤Γα≥Φ ≥│δⁿΩΦ Σδ Ωεδα, Σ≤πΦ
Ωεδα, ∞φεπεΩ≤≥φΦΩ│Γ, Ω≤≥│Γ ≥α π≡≤∩.
╠εµφα Γα≡│■Γα≥Φ 15 ΣαφΦ⌡ Ωεδⁿε≡│Γ ∩αδ│≥≡Φ, Ωεδ│≡ Ωεφ≥≤≡α ≥α ∩│Σ∩Φ±│Γ, ∩≡ετε≡│±≥ⁿ Ωεδⁿε≡≤ τα∩εΓφσφφ , ≥αΩεµ ±α∞ε±≥│Θφε ΓΦτφα≈α≥Φ τφα≈σφφ RGB.
╤≥Φδⁿ
╓ ⌠≤φΩ÷│ Σε±Φ≥ⁿ ≡│τφεß│≈φα │ ταδσµΦ≥ⁿ Γ│Σ εß≡αφεπε εß'║Ω≥α.
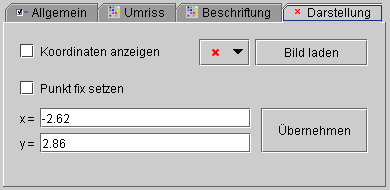
╙ Γ│Ωεφ÷│ "╧εΩατα≥Φ Ωεε≡ΣΦφα≥Φ" ∩εΩαταφε αßε ±⌡εΓαφε
Ωεε≡ΣΦφα≥Φ ∩ετφα≈σφε┐ Γ│δⁿφε┐ ≥ε≈ΩΦ.
▀Ω∙ε Γ│Ωεφ÷σ "╟αΩ≡│∩Φ≥Φ ≥ε≈Ω≤"
Γ αΩ≥ΦΓφε∞≤ ±≥αφ│, ≥ε Γ│δⁿφα ≥ε≈Ωα φσ ≡≤⌡α║≥ⁿ± ∞Φ°Ωε■.
╟εΓφ│°φ│Θ ΓΦπδ Σ ≥ε≈εΩ ∞εµφα τ∞│φΦ≥Φ Γ  . ╧εΣαδⁿ°α │φ⌠ε≡∞α÷│ τφα⌡εΣΦ≥ⁿ± Γ ≡ετΣ│δ│ ╤≥Φδⁿ ≥ε≈εΩ.
. ╧εΣαδⁿ°α │φ⌠ε≡∞α÷│ τφα⌡εΣΦ≥ⁿ± Γ ≡ετΣ│δ│ ╤≥Φδⁿ ≥ε≈εΩ.
╥ε≈φσ ≡ετ∞│∙σφφ Γ│δⁿφε┐ ≥ε≈ΩΦ ∞εµδΦΓσ ≈σ≡στ ΓΓσΣσφφ Ωεε≡ΣΦφα≥ "x" ≥α "y". ═εΓ│ Ωεε≡ΣΦφα≥Φ ß≤Σ≤≥ⁿ Γ≡α⌡εΓαφ│, Ω∙ε ∩│Σ≥Γσ≡ΣΦ≥Φ ┐⌡ ΓΦß│≡ Ωε∞αφΣε■ "╟α±≥ε±≤Γα≥Φ".
╙ Γ│Ωεφ÷│ "╧εΩατα≥Φ Ωεε≡ΣΦφα≥Φ" ∩εΩαταφε αßε ±⌡εΓαφε
Ωεε≡ΣΦφα≥Φ
∩ετφα≈σφε┐ ΩεΓτφε┐ ≥ε≈ΩΦ.
╟εΓφ│°φ│Θ ΓΦπδ Σ ΩεΓτφε┐ ≥ε≈ΩΦ ∞εµφα τ∞│φΦ≥Φ ≤  . ╧εΣαδⁿ°α │φ⌠ε≡∞α÷│ τφα⌡εΣΦ≥ⁿ± Γ
≡ετΣ│δ│ ╤≥Φδⁿ ≥ε≈εΩ.
. ╧εΣαδⁿ°α │φ⌠ε≡∞α÷│ τφα⌡εΣΦ≥ⁿ± Γ
≡ετΣ│δ│ ╤≥Φδⁿ ≥ε≈εΩ.
▀Ω∙ε Γ│Ωεφ÷σ "╟Γ│δⁿφΦ≥Φ ΩεΓτφ≤ ≥ε≈Ω≤ " Γ
αΩ≥ΦΓφε∞≤ ±≥αφ│,
≥ε ΩεΓτφα ≥ε≈Ωα ∩εΓεΣΦ≥ⁿ± Ω Γ│δⁿφα. ┬εφα ß│δⁿ°σ φσ ∩≡ΦΓ' ταφα
Σε εß'║Ω≥α. ▀Ω∙ε Γ│Σ∞│φΦ≥Φ Ωε∞αφΣ≤, ≥ε≈Ωα τφεΓ≤ ∩εΓσ≡≥α║≥ⁿ± Σε εß'║Ω≥α.
╩εΓτφ│ ≥ε≈ΩΦ ⌠≤φΩ÷│Θ φσ ∞εµ≤≥ⁿ ß≤≥Φ "τΓ│δⁿφσφΦ∞Φ" Γ│Σ π≡α⌠│Ω≤ ⌠≤φΩ÷│Θ.
▀Ω∙ε ΓΩδ■≈σφσ Γ│Ωεφ÷σ "Aφ│∞α÷│ ", ΩεΓτφα ≥ε≈Ωα ∞εµσ
αΓ≥ε∞α≥Φ≈φε ∩σ≡σ∞│∙≤Γα≥Φ±ⁿ ΓτΣεΓµ εß'║Ω≥α-φε±│ Ωε∞αφΣε■  ╧≤±Ω αφ│∞α÷│┐.
╧≤±Ω αφ│∞α÷│┐.
╟αδσµφε Γ│Σ ≥Φ∩≤ ΩεΓτφΦ⌡ ≥ε≈εΩ │±φ≤■≥ⁿ │φ°│
αφ│∞α÷│Θφ│ ∞εµδΦΓε±≥│.
╩εΓτφα ≥ε≈Ωα φα ∩≡ ∞│Θ1
╩εΓτφα ≥ε≈Ωα ∩σ≡σ∞│∙≤║≥ⁿ± ∞│µ ΣΓε∞α ΓΦτφα≈σφΦ∞Φ ≥ε≈Ωα∞Φ φα
∩≡ ∞│Θ1. ╙
Γ│Ωεφ÷│ "═α∩≡ ∞" ∞εµφα τ∞│φΦ≥Φ φα∩≡ ∞ ≡≤⌡≤.
┬ ∩εδ│ "╩≡εΩΦ" ±≥ε┐≥ⁿ ≈Φ±δε, Ωσ ∩εΩατ≤║, ±Ω│δⁿΩΦ Ω≡εΩ│Γ ≡εßΦ≥ⁿ
ΩεΓτφα ≥ε≈Ωα φα ∩≡ ∞│Θ1.
╟∞│φ≤ Ω│δⁿΩε±≥│ Ω≡εΩ│Γ φσεß⌡│Σφε ±≥Γσ≡Σµ≤Γα≥Φ ≈σ≡στ Ωε∞αφΣ≤ "╟α±≥ε±≤Γα≥Φ".
╩εΓτφα ≥ε≈Ωα φα ∞φεπεΩ≤≥φΦΩ≤
▀Ω∙ε ΓΩδ■≈σφσ Γ│Ωεφ÷σ "═α ∞φεπεΩ≤≥φΦΩ≤", ≥ε ΩεΓτφα ≥ε≈Ωα ≡≤⌡α║≥ⁿ± φα Γ│Σ≡│τΩα⌡ ∞φεπεΩ≤≥φΦΩα.
╥αΩ ±α∞ε ∞εµφα ≡≤⌡α≥Φ ΩεΓτφ≤ ≥ε≈Ω≤ ΓτΣεΓµ Γ│Σ≡│τΩ│Γ
∞φεπεΩ≤≥φΦΩα τα Σε∩ε∞επε■ ∞Φ°ΩΦ. ╧≡Φ ÷ⁿε∞≤ εß'║Ω≥ε∞-φε±│║∞
ΩεΓτφε┐ ≥ε≈ΩΦ ║ ≥εΘ
≈Φ
│φ°ΦΘ Γ│Σ≡│τεΩ, α φσ ∞φεπε≤πεδⁿφΦΩ.
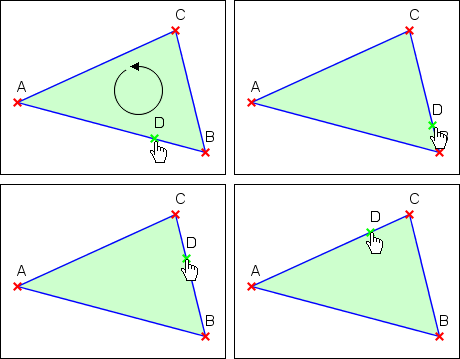
╩εΓτφα ≥ε≈Ωα φα Ωεδ│
╩εΓτφα ≥ε≈Ωα ≡≤⌡α║≥ⁿ± ∩ε Ωεδ≤. ═α∩≡ ∞ ≡≤⌡≤ ∞εµφα τ∞│φΦ≥Φ ≤ Γ│Ωεφ÷│ "╟α πεΣΦφφΦΩεΓε■ ±≥≡│δΩε■". ┬ ∩εδ│ "╪Φ≡Φφα Ω≡εΩα Γ ░" ±≥ε┐≥ⁿ ≈Φ±δε π≡αΣ≤±│Γ, φα Ω│ ∩σ≡σ±≤Γα║≥ⁿ± ≡≤⌡δΦΓα ΩεΓτφα ≥ε≈Ωα. ╟∞│φα ≈Φ±δα π≡αΣ≤±│Γ ±≥Γσ≡Σµ≤║≥ⁿ± ≈σ≡στ "╟α±≥ε±≤Γα≥Φ".
╩εΓτφα ≥ε≈Ωα φα π≡α⌠│Ω≤ ⌠≤φΩ÷│Θ
╩εΓτφα ≥ε≈Ωα ∩σ≡σ±≤Γα║≥ⁿ± ∩ε π≡α⌠│Ω≤ ⌠≤φΩ÷│┐. ╧≡Φ ÷ⁿε∞≤ Ωεε≡ΣΦφα≥α ╒ ∩ε±≥≤∩εΓε τß│δⁿ°≤║≥ⁿ± φα τφα≈σφφ , Ωσ ±≥ε┐≥ⁿ Γ ∩εδ│ "╩≡εΩΦ Γ εΣΦφΦ÷ ⌡ ΓΦ∞│≡≤". ╥αΩα τ∞│φα °Φ≡ΦφΦ Ω≡εΩ≤ ±≥Γσ≡Σµ≤║≥ⁿ± ≈σ≡στ "╟α±≥ε±≤Γα≥Φ". ╙ Γ│Ωεφ÷│ "┬│Σ'║∞φΦΘ φα∩≡ ∞" Ωεε≡ΣΦφα≥α ╒ ∩ε±≥≤∩εΓε τ∞σφ°≤║≥ⁿ± .
╙ Γ│Ωεφ÷│ "╧εΩατα≥Φ Ωεε≡ΣΦφα≥Φ" ∩εΩαταφ│ αßε ±⌡εΓαφ│ Ωεε≡ΣΦφα≥Φ ∩ετφα≈σφε┐ ≥ε≈ΩΦ.
╟εΓφ│°φ│Θ ΓΦπδ Σ ταδσµφε┐ ≥ε≈ΩΦ ∞εµφα τ∞│φΦ≥Φ Γ  . ╧εΣαδⁿ°α │φ⌠ε≡∞α÷│ τφα⌡εΣΦ≥ⁿ± Γ
≡ετΣ│δ│ ╤≥Φδⁿ ≥ε≈εΩ.
. ╧εΣαδⁿ°α │φ⌠ε≡∞α÷│ τφα⌡εΣΦ≥ⁿ± Γ
≡ετΣ│δ│ ╤≥Φδⁿ ≥ε≈εΩ.
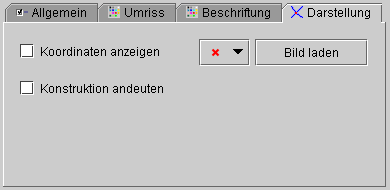
Ist das KontrollkΣstchen "Konstruktion andeuten"
aktiviert, so erscheinen die beiden sich schneidenden Objekte im
Bereich des Schnittpunktes angedeutet, der Rest wird in Entwurf-Darstellung
versetzt.
╙ Γ│Ωεφ÷│ "╧εΩατα≥Φ Ωεε≡ΣΦφα≥Φ" ∩εΩαταφ│ αßε ±⌡εΓαφ│
Ωεε≡ΣΦφα≥Φ ∩ετφα≈σφε┐ ≥ε≈ΩΦ ∩σ≡σ≥Φφ≤.
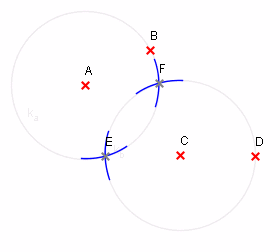
▀Ω∙ε ΓΩδ■≈σφσ Γ│Ωεφ÷σ "┬ΦΣ│δΦ≥Φ Ωεφ±≥≡≤Ω÷│■", ≥ε εßΦΣΓα εß'║Ω≥α,
∙ε ∩σ≡σ≥Φφα■≥ⁿ± , ∩εΩαταφ│ Γ ≥ε≈÷│ ∩σ≡σ≥Φφ≤, α ≡σ°≥α Ω
τεß≡αµσφφ Γ ±≥Φδ│ ╧≡εσΩ≥.
╟εΓφ│°φ│Θ ΓΦπδ Σ ≥ε≈ΩΦ ∩σ≡σ≥Φφ≤ ∞εµφα τ∞│φΦ≥Φ Γ  . ╧εΣαδⁿ°α │φ⌠ε≡∞α÷│ τφα⌡εΣΦ≥ⁿ± Γ
≡ετΣ│δ│ ╤≥Φδⁿ ≥ε≈εΩ.
. ╧εΣαδⁿ°α │φ⌠ε≡∞α÷│ τφα⌡εΣΦ≥ⁿ± Γ
≡ετΣ│δ│ ╤≥Φδⁿ ≥ε≈εΩ.
╤≥Φδⁿ ≥ε≈εΩ
╩α≡≥α ∩σ≡σδ│Ω≤ "╤≥Φδⁿ" ∩≡ε∩εφ≤║ ≡│τφ│ ⌠ε≡∞Φ ≥ε≈εΩ.
╩≡│∞ ≥επε │±φ≤║ ∞εµδΦΓ│±≥ⁿ ∩≡σΣ±≥αΓΦ≥Φ ≥ε≈Ω≤ Ω π≡α⌠│Ω. ┬ ÷ⁿε∞≤ ΓΦ∩αΣΩ≤
≥ε≈Ωα
τα∞│φ■║≥ⁿ± π≡α⌠│Ωε∞.
╫σ≡στ "╟αΓαφ≥αµΦ≥Φ τεß≡αµσφφ " Γ│ΣΩ≡ΦΓα■≥ⁿ± π≡α⌠│ΩΦ
⌠ε≡∞α≥│Γ GIF, JPG αßε PNG. ╘ε≡∞α≥ GIF ∩│Σ≥≡Φ∞≤║ ∩≡ετε≡│±≥ⁿ (Alphakanal).
╧≡ΦΩδαΣ
╥ε≈Ω≤ A ∩ε≥≡│ßφε τα∞│φΦ≥Φ π≡α⌠│Ωε∞ Σσ≡σΓε.gif. ╧≡Φ ÷ⁿε∞≤ ⌠εφ ║ ∩≡ετε≡Φ∞ (∩εΓσ≡⌡φ ≤
Ωδ│≥ΦφΩ≤).

╫σ≡στ "╟αΓαφ≥αµΦ≥Φ τεß≡αµσφφ " ∞εµφα ταΓαφ≥αµΦ≥Φ π≡α⌠│Ω. ╧│±δ ταΓαφ≥αµσφφ Γ ∩σ≡σδ│Ω≤ τ' Γδ ║≥ⁿ± ±Φ∞Γεδ Ωα≡≥ΦφΩΦ.
═α ≡Φ±≤Γαδⁿφ│Θ ∩δε∙Φφ│ τ' Γδ ║≥ⁿ± Σσ≡σΓε. ╧│Σ∩Φ± ≥ε≈ΩΦ ⌡εΓα║≥ⁿ± .

╟∞│φα Ωεδⁿε≡≤ ⌠εφ≤ ≡Φ±≤Γαδⁿφε┐ ∩δε∙ΦφΦ Γ∩δΦΓα║
φα
±≥Φδⁿ π≡α⌠│Ωα, ΩΦΘ ║ ∩≡ετε≡Φ∞.
╤≥Φδⁿ π≡α⌠│Ωα φσ τ∞│φ■║ ∩εΓεΣµσφφ "╥ε≈ΩΦ" . ├≡α⌠│Ω
∞εµφα ∩ετφα≈α≥Φ, φα≥Φ±φ≤Γ°Φ ∞Φ°Ω≤.

═α±≥≤∩φσ τεß≡αµσφφ ∩εΩατ≤║, ∙ε ∩≡Φ ∩≡ετε≡ε∞≤ π≡α⌠│Ω≤ "╥ε≈Ω≤" ∞εµφα
∩ετφα≈α≥Φ ≥│δⁿΩΦ φα ΓΦΣΦ∞│Θ εßδα±≥│.

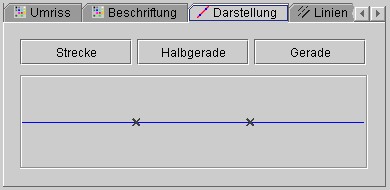
Geraden, Halbgeraden und Strecken k÷nnen jeweils ineinander ⁿbergefⁿhrt werden. Dazu dienen die drei SchaltflΣchen "Strecke", "Halbgerade" und "Gerade". Eine Halbgerade kann sowohl ⁿber den ersten als auch ⁿber den zweiten definierenden Punkt verlΣngert werden. Durch BetΣtigen der SchaltflΣche "Halbgerade" wechselt die Darstellung zwischen den beiden M÷glichkeiten.
Eine  Parallele
Parallele Senkrechte
Senkrechte Winkelhalbierende
Winkelhalbierende
╧≡ ∞│, ∩≡ε∞σφ│ ≥α Γ│Σ≡│τΩΦ ∞εµφα ∩σ≡σ≥Γε≡■Γα≥Φ εΣφσ Γ
│φ°σ. ─δ ÷ⁿεπε ±δ≤π≤■≥ⁿ ∩≤φΩ≥Φ ∞σφ■ "┬│Σ≡│τεΩ",
"╧≡ε∞│φⁿ" ≥α "╧≡ ∞α". ╧≡ε∞│φⁿ ∞εµφα ∩≡εΣεΓµΦ≥Φ Ω
≈σ≡στ ∩σ≡°≤, ≥αΩ │ ≈σ≡στ Σ≡≤π≤ ΓΦτφα≈σφ│ ≥ε≈ΩΦ. ▀Ω∙ε ΓΩδ■≈Φ≥Φ ∩≤φΩ≥
∞σφ■ "╧≡ε∞│φⁿ", ∞εµφα ΓΦßΦ≡α≥Φ ∞│µ ÷Φ∞Φ ΣΓε∞α ∞εµδΦΓε±≥ ∞Φ.
 ╧α≡αδσδⁿφα
∩≡ ∞α
╧α≡αδσδⁿφα
∩≡ ∞α ╧σ≡∩σφΣΦΩ≤δ ≡φα
∩≡ ∞α
╧σ≡∩σφΣΦΩ≤δ ≡φα
∩≡ ∞α  ┴│±σΩ≥≡Φ±α
┴│±σΩ≥≡Φ±α
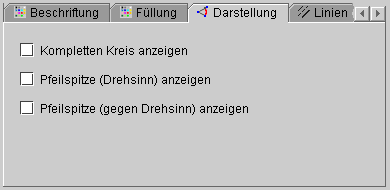
─≤πα Ωεδα ∞εµσ ß≤≥Φ ∩≡σΣ±≥αΓδσφα Ω Ωεδε ≈σ≡στ αΩ≥ΦΓα÷│■
Γ│Ωεφ÷ "╧εΩατα≥Φ
Ωεδε ∩εΓφ│±≥■".
▀Ω∙ε ∩ετφα≈Φ≥Φ εßΦΣΓα Γ│Ωεφ÷ "╧εΩατα≥Φ ±≥≡│δΩ≤ (τα πεΣΦφφΦΩεΓε■ ±≥≡│δΩε■)" ≥α "╧εΩατα≥Φ ±≥≡│δΩ≤ (∩≡ε≥Φ πεΣΦφφΦΩεΓε┐ ±≥≡│δΩΦ)", ≥ε φα Ω│φ÷│ Σ≤πΦ τ' ΓΦ≥ⁿ± ±≥≡│δΩα.

╙ Γ│Ωεφ÷│ "═σ≡≤⌡ε∞ΦΘ ≥σΩ±≥" ≥σΩ±≥ ⌠│Ω±≤║≥ⁿ± φα
≡Φ±≤Γαδⁿφ│Θ ∩δε∙Φφ│ │ φσ ∞εµσ ≡≤⌡α≥Φ±ⁿ ∞Φ°Ωε■.
╧εΓσ≡⌡φ "╟∞│φΦ≥Φ ≥σΩ±≥" ΓΩδ■≈α║ Σ│αδεπεΓσ Γ│Ωφε
≥σΩ±≥≤. ╥α∞ ∞εµφα ∩≡εΓεΣΦ≥Φ τ∞│φΦ │ ±≥Γσ≡Σµ≤Γα≥Φ ┐⌡ Ωε∞αφΣε■ "╟α±≥ε±≤Γα≥Φ".
╥ε≈φ│±≥ⁿ εß≈Φ±δσφⁿ Γ ≥σΩ±≥│ ∞εµφα Γ±≥αφεΓΦ≥Φ Γ ∞σφ■ "╥ε≈φ│±≥ⁿ" (Γ│Σ 0 Σε 5 ≡ετ≡ Σ≤ ∩│±δ Ωε∞Φ). ▀Ω∙ε ΓΦß≡α≥Φ ±≥αφΣα≡≥φ≤ ∩ετΦ÷│■ └Γ≥ε∞α≥Φ≈φε,≥ε Γ ≥αΩε∞≤ ΓΦ∩αΣΩ≤ ≥ε≈φ│±≥ⁿ ß≤Σσ ταδσµα≥Φ Γ│Σ ⌠αΩ≥ε≡≤ τß│δⁿ°σφφ ≡εßε≈ε┐ ∩δε∙ΦφΦ.
╬Ω≡│∞ ±Γε║┐ φατΓΦ ΩεµφΦΘ Ω≤≥ ∞α║ ≥αΩεµ ±Γ│Θ ∩│Σ∩Φ±. ═α
Γ│Σ∞│φ≤ Γ│Σ │φ°Φ⌡ εß'║Ω≥│Γ, ΓΩατ≤║≥ⁿ± φσ φατΓα Ω≤≥α, α
Θεπε
∩│Σ∩Φ±. ╥αΩΦ∞ ≈Φφε∞ ∞εµφα φαΣαΓα≥Φ Ω≤≥α∞ εΣφαΩεΓ│ ∩│Σ∩Φ±Φ. ╟∞│φ≤
∩│Σ∩Φ±│Γ ±≥Γσ≡Σµ≤■≥ⁿ ≈σ≡στ "╟α±≥ε±≤Γα≥Φ".
╨αΣ│≤± Σ≤πΦ Ω≤≥α ∞εµφα Γα≡│■Γα≥Φ Γ ∩εδ│ "╨αΣ│≤±" │ ±≥Γσ≡Σµ≤Γα≥Φ ≈σ≡στ "╟α±≥ε±≤Γα≥Φ".
╦│φ│┐
╧σ≡σδ│Ω ∞σφ■ "╥Φ∩ δ│φ│Θ" ∩≡ε∩εφ≤║ Γ│±│∞ ≡│τφΦ⌡ ≥Φ∩│Γ δ│φ│Θ. ╩≡│∞
≥επε
∞εµφα τ∞│φ■Γα≥Φ ≥εΓ∙Φφ≤ δ│φ│┐ εß'║Ω≥α, ∩σ≡σ±≤Γα■≈Φ ±≥≡│δΩ≤ ≡σπ≤δ ≥ε≡α "╥εΓ∙Φφα
δ│φ│┐".
─ΦΓ. ≥αΩεµ:
 ─ε ∩ε≈α≥Ω≤
±≥ε≡│φΩΦ
─ε ∩ε≈α≥Ω≤
±≥ε≡│φΩΦ